目标检测常用边框回归损失函数

04 March 2023

Paper: Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

目标检测中常用的边框回归损失函数有以下几种：

Smooth L1 Loss

Smooth L1 Loss 是 Faster R-CNN 中使用的IOU损失函数，它通过平滑L1范数来减少偏差，使训练更加稳定。当预测框与真实框之间的距离小于 1 时，损失函数采用二次函数，否则采用 L1 范数函数。其计算公式为：

$$L_{smooth}(\textbf{t}_i, \textbf{t}'_i) = \begin{cases} 0.5 (\textbf{t}_i - \textbf{t}'_i)^2, &if \ |\textbf{t}_i - \textbf{t}'_i| < 1 \\ |\textbf{t}_i - \textbf{t}'_i| - 0.5, &otherwise \ \end{cases}$$

IOU Loss

IOU Loss 是一种基于IOU（Intersection over Union）的损失函数，它计算预测框和真实框的IOU值，然后使用 1 减去 IOU 值作为损失值。其计算公式为：

$$L_{IOU} = 1 - IOU(\textbf{p}, \textbf{t})$$

• 其中，$\textbf{p}$ 是预测的边界框，$\textbf{t}$ 是真实边界框，IOU的计算公式为：

$$IOU(\textbf{p}, \textbf{t}) = \frac{\text{Area of Overlap}}{\text{Area of Union}}$$

IOU Loss的优点是简单明了，容易实现，而且对于小目标具有良好的表现。但是，IOU Loss 对于大目标的性能较差，因为它只考虑了重叠区域的面积，没有考虑距离和长宽比等因素，会出现检测框非重叠造成的梯度消失问题。

GIoU Loss

GIoU Loss 是一种基于 GIoU（Generalized Intersection over Union）的损失函数，它不仅考虑了预测框和真实框的重叠部分，还考虑了它们之间的距离和相交面积的比率。其计算公式为：

$$L_{GIoU} = 1 - IoU(\textbf{p}, \textbf{t}) + \frac{\text{Area of Enclosing Box} - \text{Area of Union}}{\text{Area of Enclosing Box}}$$

• 其中，$\text{Area of Enclosing Box}$ 是包围预测框和真实框的最小矩形面积。

缺点：

虽然 GIOU 可以解决检测框非重叠造成的梯度消失问题，但是当真实框和预测框不重叠时，GIoU 无法准确惩罚预测框，从而影响模型拟合。

具体来说，当真实框和预测框不重叠时，GIoU 会将预测框的中心点设置为真实框的中心点，将它们之间的距离作为惩罚项，但这种做法存在问题，因为此时预测框不应该被视为正确的预测。这样一来，即使预测框与真实框之间的距离很大，GIoU仍然会将它们视为有效的预测，导致误差增加。

如下图第一行为 使用GIOU 损失函数训练，模型输出的预测；而第二行为 DIOU。

DIoU Loss

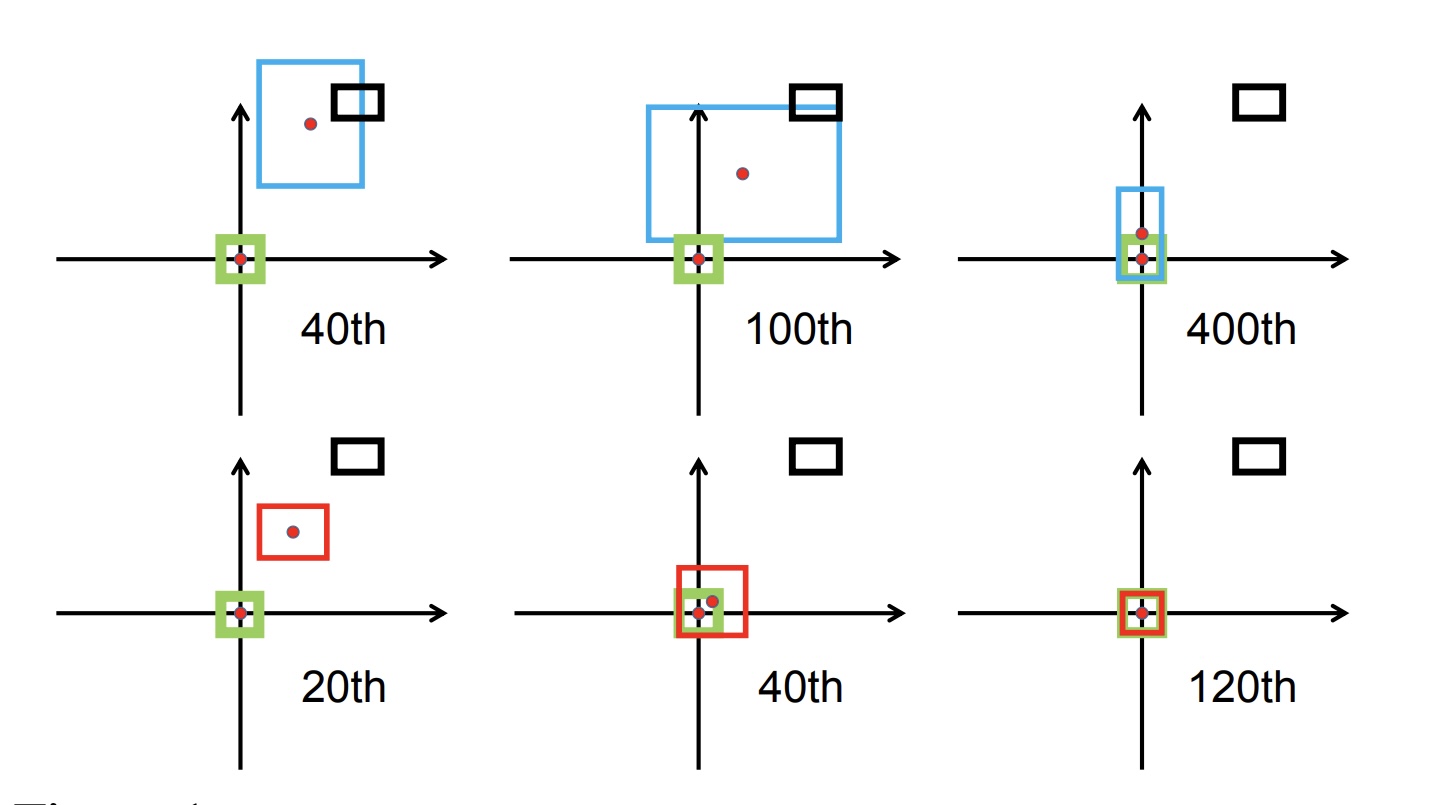
DIoU Loss 是一种基于 DIoU（Distance Intersection over Union）的损失函数，它在GIoU 的基础上加入了预测框和真实框中心点距离的惩罚项，使得预测框更加接近真实框。其计算公式为：

$$L_{DIoU} = 1 - IoU(\textbf{p}, \textbf{t}) + \frac{|\textbf{c}_p - \textbf{c}_t|^2}{\text{diag}^2(\textbf{b})}$$

• 其中，$\textbf{c}_p$ 和 $\textbf{c}_t$ 分别表示预测框和真实框的中心点，$\textbf{b}$是包围预测框和真实框的最小矩形的宽和高，$\text{diag}(\textbf{b})$ 表示对角线长度。

缺点：

1. 对于小目标的检测效果不如其他的 IoU 损失函数，因为它的惩罚项对小目标的影响较大，容易导致模型对小目标的检测效果下降。
2. 在处理长宽比差异很大的真实框和预测框时，可能会导致损失函数无法收敛。这是因为DIoU 会惩罚预测框的中心点距离真实框的中心点的距离，但是当真实框和预测框的长宽比差异很大时，这个距离可能会很大，导致损失函数无法收敛。
3. 计算复杂度较高，需要计算预测框和真实框的中心点之间的距离、宽高之间的距离、以及额外的惩罚项。这些计算在大规模的目标检测任务中会影响训练速度和效率。

CIoU Loss

CIoU Loss是一种基于 CIoU（Complete Intersection over Union）的损失函数，它在DIoU的基础上加入了预测框和真实框长宽比的惩罚项，使得预测框更加接近真实框的比例。其计算公式为：

$$L_{CIoU} = 1 - IoU(\textbf{p}, \textbf{t}) + \frac{|\textbf{c}_p - \textbf{c}_t|^2}{\text{diag}^2(\textbf{b})} + \alpha v$$

• 其中，$v$ 表示预测框和真实框长宽比之间的差异，$\alpha$ 是一个平衡因子，通常取值为2。

长宽比惩罚项 $v$的计算公式为：

$$v = \frac{4}{\pi^2}(\arccos(\frac{r}{c}) - \frac{r}{c}\sqrt{1-(\frac{r}{c})^2})$$

• 其中，$r$ 表示预测框和真实框的长宽比之间的差异，$c$ 是归一化系数。

$r$ 的计算公式为： $r = \frac{(x_{g}^{min} + x_{g}^{max})}{2} - \frac{(x_{p}^{min} + x_{p}^{max})}{2}$

• 其中，$x_{g}^{min}$ 和 $x_{g}^{max}$ 分别表示真实框和预测框在$x$轴上的最小和最大坐标，$x_{p}^{min}$ 和 $x_{p}^{max}$ 分别表示锚框和真实框在$x$轴上的最小和最大坐标。

缺点

1. CIoU损失函数中的长宽比项虽然考虑了预测框和真实框的长宽比差异，但是并没有很好地处理长宽比比较大的情况。当预测框和真实框的长宽比相差非常大时，长宽比项$v$将会非常大，从而导致整个CIoU损失函数的值非常大，这可能会影响训练的稳定性。（对目标大小、旋转敏感）
2. 计算量比 GIOU 和 DIOU 相对较大，计算过程中需要涉及多个中间变量的计算。这可能会导致训练速度较慢，尤其是在一些计算资源有限的设备上。