Batch normalization

17 March 2023

Paper: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

1. What

加速神经网络的训练
提高模型的泛化能力
避免梯度消失或爆炸等问题

2. Why

在深度神经网络中，每一层的输入数据分布往往会发生变化，尤其是在深度网络的后期，这种变化会越来越剧烈，从而导致训练过程的不稳定性，使得模型难以收敛。

3. How

$\boxed{\begin{aligned} & \textbf { Input: } \text { Values of } x \text { over a mini-batch: } \mathcal{B}=\left\{x_{1 \ldots m}\right\} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text { Parameters to be learned: } \gamma, \ \beta \\ & \textbf { Output: }\left\{y_i=\mathrm{BN}_{\gamma, \beta}\left(x_i\right)\right\} \\\\ & \ \ \ \ \ \mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^m x_i &\text {// mini-batch mean } \\ & \ \ \ \ \ \sigma_{\mathcal{B}}^2 \leftarrow \frac{1}{m} \sum_{i=1}^m\left(x_i-\mu_{\mathcal{B}}\right)^2 &\text {// mini-batch variance } \\ & \ \ \ \ \ \widehat{x}_i \leftarrow \frac{x_i-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}} &\text{// normalize }\\ & \ \ \ \ \ y_i \leftarrow \gamma \widehat{x}_i+\beta \equiv \mathrm{BN}_{\gamma, \beta}\left(x_i\right) &\text {// scale and shift } \\ \ \end{aligned}}$

Batch Normalization 的主要作用是通过对每一层的输入数据进行规范化，使得每一层的输入数据的分布都接近于标准正态分布，从而提高了训练过程的稳定性。

Batch Normalization 通常在网络中的每一层进行操作，对于每一个mini-batch中的数据，它会对其进行规范化处理，具体来说，就是对每一个输入$x_i$进行如下变换：

$\hat{x_i} = \frac{x_i - \mu_B}{\sqrt{\sigma^2 + \epsilon}}$

$\mu_B$ 和 $\sigma_B$ 分别表示一个 mini-batch 中所有数据的均值和方差，$\epsilon$ 是一个很小的数，用于避免分母为零的情况。

接着，对于每一个规范化后的数据 $\hat{x_i}$，Batch Normalization 再进行线性变换和偏置，得到输出结果：

$y_i = \gamma \hat{x_i} + \beta$

$\gamma$ 和 $\beta$ 是可学习的参数，可以通过反向传播算法进行更新。这个公式就是Batch Normalization 的主要操作流程。

Conclusion

Batch Normalization 的好处在于，它可以使得网络中每一层的输出数据分布稳定，从而加速了神经网络的收敛速度，提高了训练的效率，同时也增强了模型的泛化能力。此外，Batch Normalization 还有一些其他的优点，比如可以减小对初始权重的依赖，使得网络更容易收敛；可以缓解梯度消失或爆炸等问题，使得网络更加鲁棒。

Backforward

$\begin{aligned} \frac{\partial \ell}{\partial \widehat{x}_i} & =\frac{\partial \ell}{\partial y_i} \cdot \gamma \\ \frac{\partial \ell}{\partial \sigma_{\mathcal{B}}^2} & =\sum_{i=1}^m \frac{\partial \ell}{\partial \widehat{x}_i} \cdot\left(x_i-\mu_{\mathcal{B}}\right) \cdot \frac{-1}{2}\left(\sigma_{\mathcal{B}}^2+\epsilon\right)^{-3 / 2} \\ \frac{\partial \ell}{\partial \mu_{\mathcal{B}}} & =\left(\sum_{i=1}^m \frac{\partial \ell}{\partial \widehat{x}_i} \cdot \frac{-1}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}}\right)+\frac{\partial \ell}{\partial \sigma_{\mathcal{B}}^2} \cdot \frac{\sum_{i=1}^m-2\left(x_i-\mu_{\mathcal{B}}\right)}{m} \\ \frac{\partial \ell}{\partial x_i} & =\frac{\partial \ell}{\partial \widehat{x}_i} \cdot \frac{1}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}}+\frac{\partial \ell}{\partial \sigma_{\mathcal{B}}^2} \cdot \frac{2\left(x_i-\mu_{\mathcal{B}}\right)}{m}+\frac{\partial \ell}{\partial \mu_{\mathcal{B}}} \cdot \frac{1}{m} \\ \frac{\partial \ell}{\partial \gamma} & =\sum_{i=1}^m \frac{\partial \ell}{\partial y_i} \cdot \widehat{x}_i \\ \frac{\partial \ell}{\partial \beta} & =\sum_{i=1}^m \frac{\partial \ell}{\partial y_i} \end{aligned}$

CODE

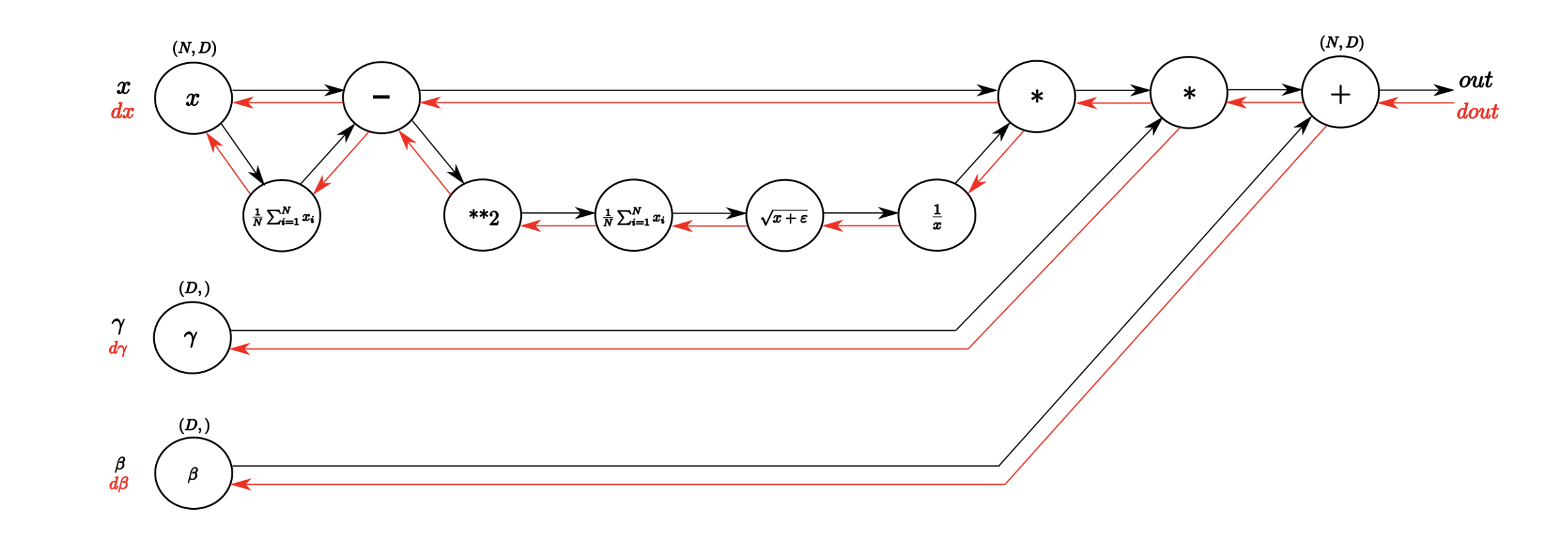
def batchnorm_forward(x, gamma, beta, eps):
    N, D = x.shape

    #step1: calculate mean
    mu = 1./N * np.sum(x, axis = 0)
    #step2: subtract mean vector of every trainings example
    x_sub_mu = x - mu
    #step3: calculate variance
    var = 1./N * np.sum(x_sub_mu**2, axis = 0)
    #step4: add eps for numerical stability, then sqrt
    sqrtvar = np.sqrt(var + eps)
    #step5: invert sqrtwar
    ivar = 1./sqrtvar
    #step6: execute normalization
    x_hat = x_sub_mu * ivar

    out =  gamma * x_hat + beta
    #store intermediate
    cache = (x_hat, gamma, x_sub_mu, ivar, sqrtvar, var, eps)

    return out, cache

def batchnorm_backward(dout, cache):

    #unfold the variables stored in cache
    x_hat, gamma, x_su b, ivar, sqrtvar, var, eps = cache

    #get the dimensions of the input/output
    N, D = dout.shape

    #step9
    dbeta = np.sum(dout, axis=0)
    dgamma_x = dout #not necessary, but more understandable

    #step8
    dgamma = np.sum(dgamma_x * x_hat, axis=0)
    dx_hat = dgamma_x * gamma

    #step7
    divar = np.sum(dx_hat * x_sub_mu, axis=0)
    dxmu1 = dx_hat * ivar

    #step6
    dsqrtvar = -1. / (sqrtvar**2) * divar

    #step5
    dvar = 0.5 * 1. /np.sqrt(var + eps) * dsqrtvar

    #step4
    dsq = 1. / N * np.ones((N, D)) * dvar

    #step3
    dxmu2 = 2 * x_sub_mu * dsq

    #step2
    dx1 = (dxmu1 + dxmu2)
    dmu = -1 * np.sum(dxmu1 + dxmu2, axis=0)

    #step1
    dx2 = 1. / N * np.ones((N,D)) * dmu

    #step0
    dx = dx1 + dx2

    return dx, dgamma, dbeta

Reference

Understanding the backward pass through Batch Normalization Layer